Welcome to Flatland
Flatland: A Romance of Many Dimensions is a satirical novel by the English educator and priest the Reverand Edwind Abbott Abbott. What was initially a satire on victorian standards and culture wound up becoming a mathematical classic, exploring the relationship between 1d, 2d, and 3d spaces. At the same time, a near-contemporary of Rev. Abbott, the famed mathematician Bernhard Reimann was making significant contributions to the world of mathematics. One such contribution is the famous “Reimann Hypothesis.” Without scaring or boring you, Reimann wanted to explore the relationship between numbers and most importantly, why prime numbers are where they are. To do so, Reimann had to explore a kind of cordinante system that you and I might not be familiar with: The complex plane.
Look at a map of a grid-based city: New york city, Chicago, or even better, Salt Lake City. When the Mormon Prophet, Brigham Young was leading his pioneers into the Salt Lake Valley, he ended up designing a city centered on a coordinate system. The center of the city would be the Salt Lake Temple, and would branch out from there.
If we were to put Temple Square at the address 0,0, then each avenue and street would follow outwards: (100 North, 300 West), (4000 South, 250 East), and so on and so forth. Many cities in Utah follow this same pattern. If I told you to meet me at 1523 N 150 E, also known as Canyon Road, you could quickly find out that I wanted to meet you at the Swig at BYU before watching a basketball game. When in Utah, do as the Utahns do I suppose.
But all of these examples I have provided teach us something that is important to linear algebra: cordinate system and visual representations of what we are doing right now!
1 Dimension: The Number Line
Start by drawing a horizontal line. On it, make a virtical mark and label it $0$. To the right of 0, make at least 5 roughly equal tick marks, and to the left, make roughly 5 equal tick marks. Label the left marks from -1 to -5 and the right marks from 1 to 5.
This is pretty easy stuff here. Pick a spot to start and draw a line with an arrow at the end to however far you want:
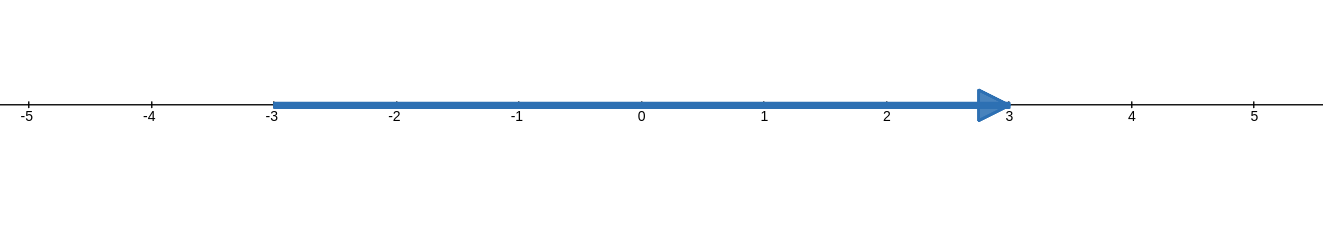
If you can’t see it, mine goes from -3 to 3, making it 6 units long. But this isn’t very exciting. You can go either right or left, extend for a finite number of spaces, or go on to infinity. You could say the domain of this space is $(-\infty,\infty)$.
Dimension 2: Cartesian Boogaloo
If you have seen Breakin’ 2, how is the back medicine treating you?
okes aside, things get more fun when we add a second dimension. Add a second vertical line to your number line at 0,0. Do the same for this new line as you did for the previous one: 5 ticks above 0 and 5 ticks below 0. Label them accordingly:
Now we can give our lovely, arrow-topped lines some room to move around. draw some new arrows and give them a starting point at (0,0):
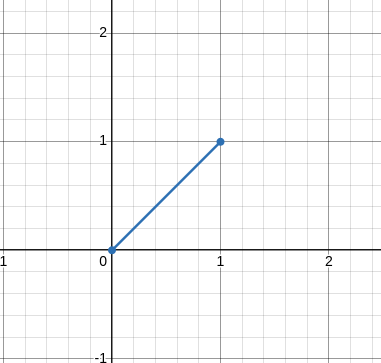
Mine doesn’t have an arrow, but hopefully you get the picture. We can measure this finite arrow by seeing how far it goes across and how high it goes. In this case, my arrow has a length of 1 and a height of 1. What does this have to do with matrices?
You put the size of the arrow into a 1 row, 2 column matrix like so:
$$ \begin{bmatrix} 1 \\ 1 \end{bmatrix}$$This type of arrow is called a vector.
We’ll look at vectors more in-depth later on, but I want you to be able to see what a matrix is visually, just to get a feel for it.
But What about Bigger Matrices?
In the case of a matrix like this:
$$ \begin{bmatrix} 5 & 8 & 2 \\ 2 & 7 & 4 \\ 1 & 9 & 2 \end{bmatrix}$$You’d either be looking at a vector that traveres many dimensions or we use matrices like these in examining networks and the lengths between points in a network. It is also useful for scatterplot data, something we care about in AI, machine learning, and higher-level statistics. As you can see, matrices have plenty of applications in the real world, which is why we are studying linear algebra in-depth! Yay you!
Multiple Vectors
We can have more than one vector on a grid. In fact, this is important to just about every field involving motion. From thermodynamics, hydrodynamics, meterology, kinsenology, plain jane physics, and plenty of others, experts use vectors to model the movement objects in 2d and 3d space. This all is possible thanks to our understanding of linear algebra.
Because of this, its important we have a strong understanding of how these vectors work, how matrices relate to vectors, and how to describe the changing of both in a logical and concrete way. From here on out, everything you will learn has a real-life application. If you have ever asked yourself the question “When am I going to use THAT in my work?”, then you should rest assured, learning linear algebra from here will greatly boost EVERYTHING you do, if you wish to become an expert in your field, even one that is creative, like music or fine arts.
This particular lesson was much shorter than most, as I just wanted to give you a taste of what you can do with vectors and linear algebra. For our next lesson, we’ll go back to our linear equations and start to build our understanding of how matrices behave in relation to linear systems.